化工过程多回路PID控制系统模式切换参数自整定

引言

化工过程一般为多变量系统，即存在着多个被控变量和多个操纵变量。随着各种化工过程先进工艺的快速发展，越来越多的生产过程被构造成多变量控制系统[1]。与单变量系统相比，多变量系统输入变量和输出变量之间一般存在一定程度的耦合，这就为多变量系统的控制器设计带来了不小的困难。对于多变量系统，设计一个包含所有被控变量和操纵变量的集中控制系统是最为理想的，但是这样的控制设计方案复杂，难以实现，不易维护，可靠性差。因此，考虑到底层控制系统安全可靠的要求，工业现场的底层控制系统仍然主要采用常规分散PID控制[2-3]，即将多变量系统分解为多个单变量子系统，分别设计PID控制回路，组成分散的多回路PID控制系统。分散多回路PID控制因其结构简单、设计和整定的简便性以及良好的鲁棒性等优点，从而在工业过程控制领域占有较大的比重。

在进行多回路PID控制系统设计时，首先确定操纵变量和被控变量的控制回路配对，然后将各PID控制回路视为单变量系统，整定PID控制参数，多回路PID控制系统设计应考虑多变量系统的操纵变量和被控变量之间存在的相互耦合作用[4]，控制系统设计应使控制回路间的耦合作用尽可能小。Bristol[5]提出了相对增益阵(relative gain array, RGA)，Wang等[6]将其推广到高维系统。在RGA中应当尽可能选择大于零且接近于1的元素对应的输入输出配对，即可保证控制回路之间的耦合最小化。为保证闭环控制系统稳定性，Niederlinski[7]提出了尼德林斯基指数(Niederlinski index, NI)，与RGA配合使用，筛选不合适的控制回路配对。由于RGA只是利用系统的稳态信息，忽略了系统的动态特性，因此在其基础上提出了各种基于动态信息的改进方法。RGA的动态改进方法大体可以分为：基于开环阶跃响应的时域RGA[8-9]、基于频率特性的频域RGA[10-11]、基于最优闭环控制器的动态RGA[12-13]、稳态信息与动态信息结合的组合RGA[14-17]。虽然RGA及其改进方法在一定程度上解决了常规控制系统结构设计问题，但是控制系统性能还与控制器参数有关。由于系统内部耦合作用的存在，其他回路的控制器参数必定对本回路的等效被控对象产生影响[18]。在实际工业现场，由于种种工艺需求，操作人员往往需要对控制回路进行手动/自动切换。当其他回路开环/闭环切换时，本回路的等效被控对象必然发生变化，本回路的PID控制器参数应当进行相应的调整以适应本回路被控对象动态特性的变化，才能保证稳定性并维持一定的控制性能。

本文将利用现代频域法，从多变量系统对角优势下正Nyquist稳定性判据的角度考虑，进行控制回路模式切换时的控制器参数校正工作。目前现代频域法的控制系统设计从单变量系统推广到了多变量系统[19-20]。Nyquist阵列设计法是现代多变量频域设计法中最成熟的一种方法。Rosenbrock等[21-23]论述了Nyquist阵列设计法的基本思想，为后续研究提供了基本研究方法。在此基础上，McMorran[24-25]提出了逆Nyquist阵列设计的扩展方法。Ho等[26]和Chen等[27]提出了正Nyquist阵列设计方法。Nyquist阵列设计法往往与Gershgorin带结合使用，Gershgorin带可以同时判断控制系统的对角优势和闭环稳定性，Chen等[28]利用Gershgorin带定理对多变量系统完成了PID控制器参数设计。

常规PID控制的整定算法一般只是针对单变量系统。Luyben[29]提出了著名的BLT方法，即利用Z-N规则来调整PID参数，Ho等[30]提出了基于增益和相角裕量的设计方法。多变量分散PID控制中控制回路模式切换时控制器参数的校正问题尚无研究。

本文基于对角优势下正Nyquist稳定判据，从Gershgorin圆边界点的角度分析系统的稳定性，根据闭环稳定性进一步确定控制器增益的调整方向及程度，以保证控制回路在切换前后的闭环稳定性。

1 控制回路模式切换问题

对于一个存在内部耦合的多变量化工过程，考虑到化工过程多回路PID控制系统模式切换时对实时性和实际工业现场操作人员对可操作性的要求，本文采用了工业过程控制中常用的一阶惯性纯滞后的传递函数矩阵 G (s)形式，如式(1)所示。

G(s)=⎡⎣⎢⎢⎢⎢⎢g11(s)g21(s)⋮gn1(s)g12(s)g22(s)⋮gn2(s)⋯⋯⋱⋯g1n(s)g2n(s)⋮gnn(s)⎤⎦⎥⎥⎥⎥⎥$G\left(s\right)=\left(\begin{array}{cccc}{g}_{11}\left(s\right)& g_{12}\left(s\right)& \cdots & g_{1n}\left(s\right)\\ g_{21}\left(s\right)& g_{22}\left(s\right)& \cdots & g_{2n}\left(s\right)\\ ⋮& ⋮& \ddots & ⋮\\ g_{n1}\left(s\right)& g_{n2}\left(s\right)& \cdots & g_{nn}\left(s\right)\end{array}\right)$(1)

其中

gij(s)=kije−τijsTijs+1(i, j=1, 2, 3, ⋯, n)$\begin{array}{cc}{g}_{ij}\left(s\right)=\frac{k_{ij}{e}^{-{\tau }_{ij}s}}{T_{ij}s+1}& (i,j=1,2,3,\cdots ,n)\end{array}$

式中，s为复变量。

式(1)为系统稳态点附近的线性化模型，具有形式简单、适用性强、易于获取的特点，并且在定值控制系统中各变量都不会偏离稳态点太远，因此精度也能满足控制系统设计要求。

工业现场经验丰富的工艺人员很容易获取这种一阶惯性纯滞后模型，他们一般都能知晓各输入变量对各输出变量的静态增益k，以及当输入变量发生变化后输出变量多长时间才能变化和多长时间到达稳定状态，分别对应纯滞后时间τ和动态响应时间ts，由此可以计算得到时间常数T（动态响应时间ts减掉纯滞后时间τ后再除以3或4）。

对于由式(1)表示的化工过程，其控制方式可以分为两种：集中控制和分散控制。

集中控制采用单个控制器，变量之间仅一种配对方式，其控制效果较好，但直接设计集中控制器的难度较大。一般设计单个解耦器和多个控制器作为集中控制器[31]，变量之间采用对角配对方式，控制效果与解耦效果相关，其控制结构如图1所示。

图1

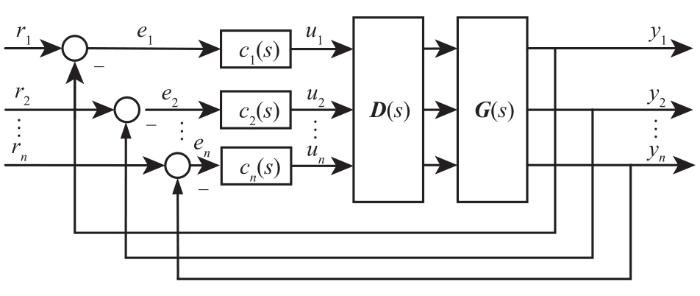
图1   多变量解耦控制

Fig.1   Multivariable decoupling control