基于热扩散核密度确定密度峰值法的历史工况识别

引 言

近年来，随着物联网、大数据和人工智能等技术的兴起，数据驱动的方法在工业智能化的进程中扮演着重要角色。在实际生产过程中，原料性质、生产方案或操作条件等因素的变动将导致生产过程的多模态化[1]，如发酵过程[2]、冶金过程和锅炉燃烧过程等，对其过程进行数字化时往往存在着非线性、多模态和变量间的强相关性等问题[3-4]。因此，深入研究多模态过程的特点对实际生产有着重要作用。通过获取历史工况特征，不仅可以为当前装置选择合适的工况模型及参数进行优化，也能为生产决策提供重要的数据参考，如污水处理装置的智能优化、管道泄漏的自动化检测和生产运行状况的有效评估[5-6]等。

在对多模态过程的研究中，由于不同工况间存在着较大的差异，研究者通常假设每种工况下的过程数据近似服从一种高斯分布，运用主成分分析（PCA）、偏最小二乘（PLS）、独立成分分析（ICA）和支持向量数据描述（SVDD）模型等方法提取工况数据的特征，然后建立模型应用于过程故障检测、过程控制和过程优化等[7-10]。由于每种工况下的数据具有相似性，有学者将数据聚类的方法用于多模态过程的特征提取[11]。常用的聚类方法包括模糊C均值法[12]、K-均值法[13]、高斯混合模型（GMM）[14-15]和隐马尔可夫模型（HMM）[16]等，这些方法在获取数据特征时具有一定的有效性，但仍存在一些无法避免的缺陷。如K-均值法需要事先确定聚类数量，对数据中的噪声点敏感；模糊C均值法存在聚类数量和参数选取的问题；HMM模型需要事先知道各种模态的概率且固定不变；GMM模型在使用期望最大法求解时，存在计算量较大、对模型参数的初值敏感和容易陷入局部极值等问题，这些缺点都将导致无法准确地识别工况[17-18]。有学者对GMM模型进行深入研究，提出了给定模型参数初值[19]和基于信息准则确定聚类数量[20]的方法，其中F-J的方法较为著名[21-22]，它通过在迭代计算中不断剔除冗余的高斯分量得出聚类结果，但是该方法需要一个较大的聚类数量导致计算量大且收敛困难，其结果的准确性也不能保证。

快速搜索发现密度峰[23]（CFSFDP）是基于局部密度的一种聚类技术，它根据聚类中心点密度较大且与其他中心点距离较远的特点，引入高斯核密度估计函数（KDE）计算数据点的密度，再通过欧氏距离计算数据点间的距离，从而完成数据聚类。但是该方法的聚类效果取决于截距参数，为避免这一点，有学者对其进行改进并提出了无须事先确定截距参数的热扩散核密度确定密度峰的技术[24]（CFSFDP-HD）。本文提出将CFSFDP-HD技术与GMM模型结合的方法，首先通过CFSFDP-HD方法对多模态过程数据进行聚类，然后将聚类结果作为GMM模型的初值，从而对多模态过程的工况进行较准确的估计。

1 工况识别方法

1.1 高斯混合模型

过程数据 X n×d 是d维的n个样本数据，且X={x1,x2,⋯,xn}$X=\left(x_1,x_2,\cdots ,x_n\right)$，其概率密度函数可表示为：

p(x|θ)=∑i=1kτig(x|θi)$p\left(x|\theta \right)=\sum _{i=1}^k{\tau }_{i}g\left(x|{\theta }_i\right)$(1)

其中，k为高斯模型的数量，τi 和θi={μi,Σi}${\theta }_i=\left({\mu }_i,{\Sigma }_i\right)$分别为第i个高斯模型的权重和参数（平均值和协方差）。

第i个高斯模型对应的高斯密度函数为：

g(x|θi)=1(2π)d/2|Σi|1/2exp[−12(x−μi)TΣ−1i(x−μi)]                         (i=1,2,⋯,k)$\begin{array}{c}g\left(x|{\theta }_i\right)=\frac{1}{{\left(2\pi \right)}^{d/2}{\left({\Sigma }_i\right)}^{1/2}}exp\left(-\frac{1}{2}{\left(x-{\mu }_i\right)}^{{\rm T}}{\Sigma }_i^{-1}\left(x-{\mu }_i\right)\right)\\ \left(i=\mathrm{1,2},\cdots ,k\right)\end{array}$(2)

模型的参数θi 常用EM法[25]求解，通过不断地更新后验概率和模型参数，直到模型参数几乎不变。针对数据X={x1,x2,⋯,xn}$X=\left(x_1,x_2,\cdots ,x_n\right)$和模型初始参数θ(0)={{τ(0)1,θ(0)1},{τ(0)2,θ(0)2},…,{τ(0)k,θ(0)k}}${\theta }^{\left(0\right)}=\left(\left({\tau }_1^{\left(0\right)},{\theta }_1^{\left(0\right)}\right),\left({\tau }_2^{\left(0\right)},{\theta }_2^{\left(0\right)}\right),\dots ,\left({\tau }_k^{\left(0\right)},{\theta }_k^{\left(0\right)}\right)\right)$，其迭代计算步骤如下。

E步骤：

P(s)(Ck|xj)=τ(s)kg(xj|μ(s)k,Σ(s)k)∑i=1kτ(s)ig(xj|μ(s)i,Σ(s)i)         (j=1,2,⋯,n)$P^{\left(s\right)}\left(C_k|x_j\right)=\frac{{\tau }_k^{\left(s\right)}g\left(x_j|{\mu }_k^{\left(s\right)},{\Sigma }_k^{\left(s\right)}\right)}{\sum _{i=1}^k{\tau }_i^{\left(s\right)}g\left(x_j|{\mu }_i^{\left(s\right)},{\Sigma }_i^{\left(s\right)}\right)}\left(j=\mathrm{1,2},\cdots ,n\right)$(3)

P(s)(Ck|xj)$P^{\left(s\right)}\left(C_k|x_j\right)$表示第j个样本属于第k个高斯模型的后验概率，s表示第s次迭代。

M步骤：

μ(s+1)k=∑j=1nP(s)(Ck|xj)xj∑j=1nP(s)(Ck|xj)${\mu }_k^{\left(s+1\right)}=\frac{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)x_j}{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)}$(4)Σ(s+1)k=∑j=1nP(s)(Ck|xj)(xj−μ(s+1)k)(xj−μ(s+1)k)T∑j=1nP(s)(Ck|xj)${\Sigma }_k^{\left(s+1\right)}=\frac{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)\left(x_j-{\mu }_k^{\left(s+1\right)}\right){\left(x_j-{\mu }_k^{\left(s+1\right)}\right)}^{{\rm T}}}{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)}$(5)τ(s+1)k=∑j=1nP(s)(Ck|xj)n${\tau }_k^{\left(s+1\right)}=\frac{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)}{n}$(6)

其中，μ(s+1)k、Σ(s+1)k、τ(s+1)k${\mu }_k^{\left(s+1\right)}、{\Sigma }_k^{\left(s+1\right)}、{\tau }_k^{\left(s+1\right)}$分别为第k个高斯模型在第（s+1）次迭代的平均值、协方差矩阵和先验概率。

基于最短信息长度准则的F-J方法只需对式（6）进行如下修改，即可得到较为理想的聚类结果。

τ(s+1)k=max{0,(∑j=1nP(s)(Ck|xj))−v2}∑i=1kmax{0,(∑j=1nP(s)(Ck|xj))−v2}${\tau }_k^{\left(s+1\right)}=\frac{max\left(0,\left(\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)\right)-\frac{v}{2}\right)}{\sum _{i=1}^{k}max\left(0,\left(\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)\right)-\frac{v}{2}\right)}$(7)

其中，v=12d2+32d$v=\frac{1}{2}{d}^2+\frac{3}{2}d$，d为变量的个数，通过迭代将任意两个相同的高斯模型进行合并，最终获得多个工况模型及其参数。

1.2 热扩散核密度确定密度峰技术

基于热扩散的高斯核函数为：

P(di,dj,t)=1n∑j=1n12πt√e−(di−dj)22t$P\left(d_i,d_j,t\right)=\frac{1}{n}\sum _{j=1}^n\frac{1}{\sqrt[]{2\pi t}}{e}^{-\frac{{\left(d_i-d_j\right)}^2}{2t}}$ （j =1,2,…,n）(8)

P(di,dj,t)$P\left(d_i,d_j,t\right)$为样本点i到j的转移概率，t为核函数的带宽，di - dj 为样本j到i的距离。

估算任意样本点i的概率密度函数为：

ρi=f⌢(d;t)≈∑k=0n−1αke−k2π2t/2cos(kπd)${\rho }_i=\stackrel{⌢}{f}\left(d;t\right)\approx \sum _{k=0}^{n-1}{\alpha }_k{e}^{-k^2{\pi }^{2}t/2}cos\left(k\pi d\right)$(9)

式（9）为KDE的完全自适应形式，考虑了最佳带宽选择和边界校正。其中n为一个较大的整数，本文取n为样本数量，αk 为：

αk=⎧⎩⎨⎪⎪⎪⎪1,k=01n∑i=1ncos(kπdi),k=1,2,⋯,n−1${\alpha }_k=\left(\begin{array}{c}\begin{array}{cc}1,& k=0\end{array}\\ \begin{array}{cc}\frac{1}{n}\sum _{i=1}^{n}cos\left(k\pi d_i\right),& k=\mathrm{1,2},\cdots ,n-1\end{array}\end{array}\right)$(10)

最佳带宽的选择使用了改进的Sheather–Jones(ISJ)方法[26]，其计算步骤如下：

t=ξγ[l](t)$t=\xi {\gamma }^{\left(l\right)}\left(t\right)$(11)ξ=62√−37$\xi =\frac{6\sqrt[]{2}-3}{7}$(12)γ[l](t)=γ1(γ2(⋯γl(t)⋯))${\gamma }^{\left(l\right)}\left(t\right)={\gamma }_1\left({\gamma }_2\left(\cdots {\gamma }_l\left(t\right)\cdots \right)\right)$(13)γ[l](t)=1+0.5(l+0.5)31×3×⋯×(2l−1)nπ/2√∥∥f(l+1)∥∥2${\gamma }^{\left(l\right)}\left(t\right)=\frac{1+0.5^{\left(l+0.5\right)}}{3}\frac{1\times 3\times \cdots \times \left(2l-1\right)}{n\sqrt[]{\pi /2}{\left(f^{\left(l+1\right)}\right)}^2}$(14)∥∥f(l+1)∥∥2=∑k=1l−1(kπ)(2l+2)α2kexp(−(kπ)2t)${\left(f^{\left(l+1\right)}\right)}^2={\sum _{k=1}^{l-1}\left(k\pi \right)}^{\left(2l+2\right)}{\alpha }_k^{2}exp\left(-{\left(k\pi \right)}^{2}t\right)$(15)

其中，当l ≥ 5时，l的取值对式（11）的计算结果影响很小，故本文中取l = 5。

带宽t的详细求解步骤如下：

（1）设置一个较小的容差ε = 10-9，令yq=ε，q = 0；

（2）计算yq+1=ξγ[l](yq)$y_{q+1}=\xi {\gamma }^{\left(l\right)}\left(y_q\right)$；

（3）如果∣∣yq+1−yq∣∣<ε$\left(y_{q+1}-y_q\right)<\epsilon$，t = yq+1停止，否则yq = yq+1，q = q +1，返回步骤（2）。另外，令t = sqrt(t)/3.3，可对边界点进行修正。

计算每一样本点i到最近的高密度点j的距离：

δ={min(dij), if ∃ j, ρj>ρimax(dij), otherwise$\delta =\left(\begin{array}{c}min\left(d_{ij}\right),if\exists j,{\rho }_j>{\rho }_i\\ max\left(d_{ij}\right),otherwise\end{array}\right)$(16)

1.3 提出方法的计算步骤

本文提出的方法对近似服从高斯分布的未知多模态稳态工况进行识别时，首先利用CFSFDP-HD技术对多模态过程数据进行聚类，确定聚类中心点及其个数（即工况个数），然后将每一类数据的平均值和协方差作为GMM模型的初值，迭代求出不同工况的特征参数。其计算过程如下：

（1）将数据标准化处理，求取参数αk；

（2）由参数αk 和式（11）~式（15）得出最佳带宽t；

（3）由式（9）和式（16）的结果画出决策图，并由此完成聚类；

（4）将每一类的特征参数作为GMM模型初值，求出最终工况参数。

通过以上步骤即可完成对历史工况的准确识别，下面通过第2节中的两个例子对该方法进行验证。

图1

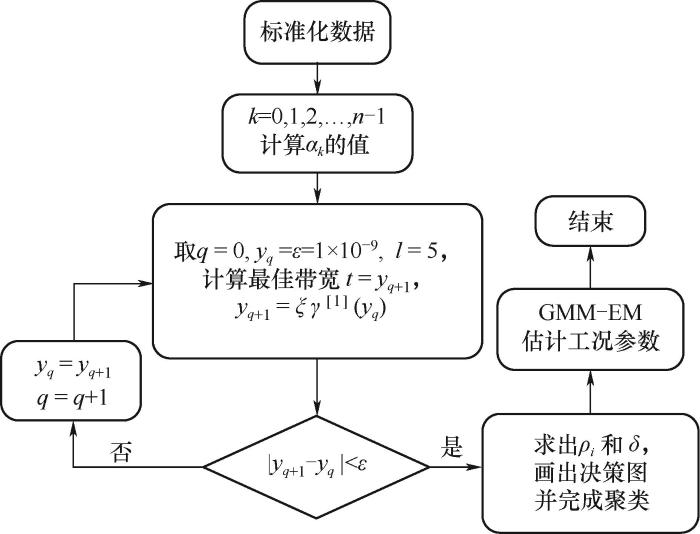
图1   基于热扩散核密度的工况识别方法流程图

Fig.1   Flow chart of recognizing operating modes based on kernel density estimation of heat diffusion