CO2混合工质的气液相平衡的混合规则对比与预测研究

引言

二氧化碳(CO2)属于自然工质，由于其高热稳定性、安全环保并且高能量密度实现部件小型化等优点，使得CO2动力循环在新一代热功转化循环、内燃机余热、中低温热能、火电、核电和太阳能利用等领域具有广泛的应用前景。同时CO2作为循环介质，也是一种对CO2的直接资源化利用方式，符合国家双碳政策，但是CO2纯工质循环运行压力高，应用中存在安全隐患，且临界温度较低对冷源要求很高[1]。碳氢类(HCs)工质虽能提高能源利用效率，但HCs易燃易爆；氢氟烃类工质(HFCs)的全球变暖潜能值（GWP）偏高，不符合《〈蒙特利尔议定书〉基加利修正案》的要求[2]；氢氟烯烃类工质(HFOs)汽化潜热低，热力性能较差。因此很难找到性能优异、热稳定性高又对环境友好安全的纯工质，而CO2混合工质动力循环通过不同的组分配比，可以实现既能提高能源利用效率又能对环境友好的要求。CO2+HCs混合工质可以消除可燃性，降低易燃易爆的风险；CO2+HFCs混合工质可以降低GWP值；CO2+HFOs混合工质可以提高工质的热力性能。

Bell等[3]总结了目前能作为制冷工质的各类混合工质的气液相平衡实验数据，其中CO2混合工质的气液相平衡实验数据有21种。混合工质气液相平衡理论计算的重点是选择合适的混合规则，提高计算精度，混合规则的形式各种各样，包括vdW混合规则、WS混合规则、MHV1混合规则等。各类CO2混合工质适用于何种混合规则没有明确给出，Kim等[4]对于CO2+propane混合工质使用vdW混合规则计算；对于CO2+HFC-134a混合工质，Duran-Valencia等[5]使用vdW混合规则计算气液相平衡数据，而Lim等[6]和Silva-Oliver等[7]选择的是WS混合规则；Valtz等[8-9]选择WS混合规则计算了CO2+HFC-152a和CO2+HFC-227ea的气液相平衡数据；对于CO2+HFO-1234yf混合工质，Juntarachat等[10]使用vdW混合规则计算气液相平衡数据；而Wang等[11]使用了WS混合规则计算了CO2+HFO-1234ze(E)混合工质。综上所述，目前各类CO2混合工质使用的混合规则形式不统一，系统分析不同混合规则形式对于各类CO2混合工质的适用性具有重要意义。另外，由于气液相平衡实验需要耗费大量的时间和精力，因此提出适合CO2混合工质气液相平衡的预测模型，也是一项具有重大意义的工作。

本文结合CO2混合工质动力循环的应用背景，选取出11种 CO2混合工质的气液相平衡实验数据，包括7种CO2+HFCs/HFOs二元体系和4种 CO2+HCs二元体系。选用PR方程结合三种不同形式的混合规则(vdW、WS、MHV1)计算这11种二元体系的气液相平衡数据，并与各体系公开发表的文献实验值相比较，得出计算结果与实验数据之间的相对偏差，从而分析与讨论不同混合规则对于各类CO2混合工质的适用性。最后提出一种差值模型，对CO2混合工质气液相平衡模型进行了预测。

1 气液相平衡的理论基础公式

气液相平衡性质反映的是流体气液两相之间的相互关系，描述的是混合物气液平衡时，其温度T、压力p和气相组分yi 、液相组分xi 之间的关系。气液相平衡理论需要状态方程结合混合规则与活度系数模型描述得出。

1.1 PR状态方程

本文采用PR方程作为计算混合工质气液相平衡的基础。PR方程由Peng和Robinson在1976年提出[12]，其表达式为：

p=RTv−b−av(v+b)+b(v−b)$p=\frac{RT}{v-b}-\frac{a}{v(v+b)+b(v-b)}$(1)

式中，a$a$和b$b$是状态方程系数，可由临界参数和偏心因子计算得到：

a=0.45724R2T2cpcα(T)$a=0.45724\frac{R^2{T}_c^2}{p_c}\alpha \left(T\right)$(2)b=0.0778RTcpcα(T)$b=0.0778\frac{R{T}_c}{p_c}\alpha \left(T\right)$(3)

α(T)$\alpha \left(T\right)$函数定义为：

α(T)=[1+(0.37646+1.54226ω−0.26992ω)(1−T0.5r)]22$\alpha \left(T\right)=[1+(0.37646+1.54226\omega -0.26992\omega {}_{}{}^2\left)\right(1-T{}_r^{0.5}){]}^2$(4)

状态方程被用于描述混合工质的热力学性质时，需要引入混合规则。

1.2 混合规则

1.2.1 vdW混合规则

描述混合工质的热力学性质时，vdW[13]混合规则被广泛应用，作为一种常数型混合规则，其形式如下：

am=∑i∑jxixjaij$a_m=\sum _i\sum _j{x}_i{x}_j{a}_{ij}$(5)bm=∑ixibi$b_m=\sum _i{x}_i{b}_i$(6)aij=aiaj−−−−√(1−kij)$a_{ij}=\sqrt[]{a_i{a}_j}(1-k_{ij})$(7)

1.2.2 MHV1混合规则

MHV1混合规则是Michelsen[14]对HV[15]混合规则进行改进得到的，其是一种经典的GE-EOS混合规则, 以零压为参考态，具体形式如下：

ambmRT=∑ixiaibiRT+1q1O$\frac{a_m}{b_{m}RT}=\sum _i{x}_i\frac{a_i}{b_{i}RT}+\frac{1}{q_1}O$(8)bm=∑ixibi$b_m=\sum _i{x}_i{b}_i$(9)O=GERT+∑ixiln(bmbi)$O=\frac{G^E}{RT}+\sum _i{x}_{i}ln\left(\frac{b_m}{b_i}\right)$(10)

1.2.3 WS混合规则

Wong和Sandler于1992年提出Wong-Sandler(WS)混合规则[16]，该法则基于超额Helmholtz自由能，与密度无关且满足第二维里系数边界条件, 其形式如下：

bm=∑i∑jxixj(b−aRT)ij1−GECRT−∑ixi(aiRTbi)$b_m=\frac{\sum _i\sum _j{x}_i{x}_j{\left(b-\frac{a}{RT}\right)}_{ij}}{1-\frac{G^E}{CRT}-\sum _i{x}_i\left(\frac{a_i}{RT{b}_i}\right)}$(11)(b−aRT)ij=12[(b−aRT)i+(b−aRT)j](1−kij)${\left(b-\frac{a}{RT}\right)}_{ij}=\frac{1}{2}\left({\left(b-\frac{a}{RT}\right)}_i+{\left(b-\frac{a}{RT}\right)}_j\right)(1-k_{ij})$(12)ambm=∑ixiaibi+GEC$\frac{a_m}{b_m}=\sum _i{x}_i\frac{a_i}{b_i}+\frac{G^E}{C}$(13)

三种混合规则各有优势，WS和MHV1混合规则对高度非理性体系和强极性体系有着非常好的描述能力；而vdW混合规则只有一个交互参数，形式简单，具有较强的物理意义。

1.3 活度系数模型

1968年Renon和Prausnitz[17]修正了溶液局部组成表达式, 在双流体理论的基础上提出了NRTL活度系数模型,其能很好地描述二元体系的相平衡性质, 对于常见的二元系统其表达式为:

GERT=x1x2(τ21G21x1+x2G21+τ12G12x1+x1G12)$\frac{G^E}{RT}=x_1{x}_2\left(\frac{{\tau }_{21}{G}_{21}}{x_1+x_2{G}_{21}}+\frac{{\tau }_{12}{G}_{12}}{x_1+x_1{G}_{12}}\right)$(14)G12=exp(−α12τ12),G21=exp(−α21τ21)$G_{12}=exp(-{\alpha }_{12}{\tau }_{12}),G_{21}=exp(-{\alpha }_{21}{\tau }_{21})$(15)

组分1、2的活度系数方程为:

lnγ1=x22[τ21G221(x1+x2G21)2+τ12G12(x2+x1G12)2]$ln{\gamma }_1=x_2^2\left(\frac{{\tau }_{21}{G}_{21}^2}{(x_1+x_2{G}_{21}{)}^2}+\frac{{\tau }_{12}{G}_{12}}{(x_2+x_1{G}_{12}{)}^2}\right)$(16)lnγ2=x21[τ12G212(x2+x1G12)2+τ21G21(x1+x2G21)2]$ln{\gamma }_2=x_1^2\left(\frac{{\tau }_{12}{G}_{12}^2}{(x_2+x_1{G}_{12}{)}^2}+\frac{{\tau }_{21}{G}_{21}}{(x_1+x_2{G}_{21}{)}^2}\right)$(17)

2 混合物气液相平衡计算

三种混合规则中的相互作用参数需要结合实验数据，使用目标函数优化计算得出。本文的目标函数综合考虑了压力计算相对偏差与气相组分浓度绝对偏差，如下所示：

OF=1N∑i=1N[(pexp−pcalpexp)2+(y1,exp−y1,cal)2]12$OF=\frac{1}{N}{\sum _{i=1}^N\left({\left(\frac{p_{exp}-p_{cal}}{p_{exp}}\right)}^2+{\left(y_{1,exp}-y_{1,cal}\right)}^2\right)}^{\frac{1}{2}}$(18)AARD(p)=1N∑i=1N∣∣pexp−pcalpexp∣∣×100%$AARD\left(p\right)=\frac{1}{N}\sum _{i=1}^N\left(\frac{p_{exp}-p_{cal}}{p_{exp}}\right)\times 100\%$(19)AAD(y)=1N∑i=1N∣∣y1,exp−y1,cal∣∣$AAD\left(y\right)=\frac{1}{N}\sum _{i=1}^N\left(y_{1,exp}-y_{1,cal}\right)$(20)

本文分别在CO2/HFCs、CO2/HFOs和CO2/HCs二元体系中选取了CO2(1)+HFC-152a(2)[9]、CO2+HFO-1234ze(E)[11]、CO2+propane[4]三类混合工质，给出了不同混合规则的比较。

2.1 CO2+HFC-152a混合工质各种混合规则对比

CO2(1)+ HFC-152a(2)混合工质的压力相对偏差、气相摩尔分数绝对偏差以及p-x-y曲线如图1、图2所示，其中图2中的散点表示不同温度下的气液相平衡的实验点，从图中可以看出对于CO2(1)+ HFC-152a(2)混合工质，WS+NRTL混合规则压力相对偏差的绝对值在1%以内，气相摩尔分数绝对偏差的绝对值在0.01以内，其计算精度最高；在低于CO2临界温度304.13 K的温区(亚临界区域)，三种混合规则计算精度相差不大，但在高于CO2临界温度的温区(超临界区域)，WS+NRTL混合规则的优势就体现了出来，这是因为WS混合规则对高度非理性体系和强极性体系有着非常好的描述能力。

图1

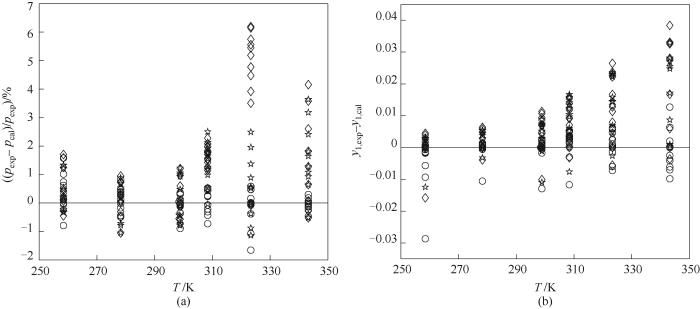
图1   CO2(1)+HFC-152a(2)的压力相对偏差与气相摩尔分数绝对偏差

○ WS+NRTL; ☆ MHV1+NRTL; ◇ vdW

Fig.1   The relative deviation of the pressure and the absolute deviation of the component mole fraction of CO2 (1) + HFC-152a (2)